|
Calcularis
Rechenschwäche mit Hilfe von Rechnern begegnen
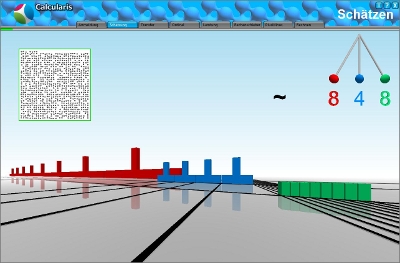
Abbildung 1: Gesamtansicht einer Schätzaufgabe
Inhalt
Stand der Forschung
Calcularis ist eine neue Trainings-Software zur Verbesserung von Zahlenverständnis und Rechenfertigkeiten. Es eignet sich insbesondere für Kinder, die beim Rechnenlernen Schwierigkeiten haben. Calcularis ist eine Weiterentwicklung des Programms «Rette Calcularis», dessen Effektivität bereits in einer Studie wissenschaftlich nachgewiesen wurde (Kucian et al., 2011). Das Training verbessert die Entwicklung der Zahlenraumvorstellung, es erleichtert das arithmetische Denken und entlastet das Arbeitsgedächtnis.
Das Konzept von Calcularis basiert auf aktuellen neurowissenschaftlichen Erkenntnissen der Zahlenverarbeitung sowie der mathematischen Entwicklung bei Kindern (Triple-Code-Modell, Dehaene, 1992; Vier-Stufen-Entwicklungsmodell, von Aster & Shalev, 2007).
Struktur des Trainings
Die Struktur dieses Trainings ist strikt hierarchisch nach drei grösser werdenden Zahlenräumen aufgebaut (0-10, 0-100, 0-1000). Jeder Zahlenraum umfasst zwei Bereiche:
- Zahlendarstellung und -verständnis: In jedem Zahlenraum muss immer zuerst das numerische Verständnis gebildet werden. Von der konkreten Darstellung ausgehend, wird dabei zuerst die Zahlwort-Darstellung, dann die arabische Schreibweise und schliesslich noch die Darstellung der Zahl auf dem Zahlenstrahl eingeführt. Zusätzlich zu diesen verschiedenen Repräsentationen, wird in diesem Bereich auch das Verständnis von Zahlen gefördert. Eine Zahl kann als Kardinalzahl (Anzahl von Objekten), als Ordinalzahl (Position in einer Reihe) oder als Relationalzahl (Beziehung zwischen zwei Zahlen) verstanden werden. Diese drei Aspekte werden eingeführt und mit verschiedenen Spielen vertieft.
- Arithmetische Operationen: Mathematisches Verständnis bedeutet nicht nur, die verschiedenen Zahlenrepräsentation zu kennen, sondern auch, Operationen (z.B. Additionen und Subtraktionen) mit Zahlen durchzuführen. Die Schwierigkeit der gestellten Aufgaben ist dabei von verschiedenen Komponenten abhängig. Einerseits ist das die numerische Grösse der Zahlen, andererseits hängt die Schwierigkeit aber auch davon ab, wie die Aufgabe präsentiert wird (Zahlendarstellung) und ob Hilfsmittel zur Lösung verwendet werden können. Im Bereich arithmetische Operationen, werden also nicht nur Operationen mit Zahlen geübt; es findet gleichzeitig eine Vertiefung und Automatisierung der verschiedenen Zahlendarstellungen sowie des Zahlenverständnisses statt.
Für beide Bereiche gibt es passende Spiele, jeweils ein sogenanntes Hauptspiel und die Unterstützungsspiele. Die Letztgenannten sind Vorläuferspiele für die Hauptspiele, sie trainieren Fähigkeiten, die in den Hauptspielen benötigt werden.
Anpassung an den Benutzer
Alle Kinder beginnen das Training mit dem einfachsten Spiel im Zahlenraum von 0-10. Je nach Fähigkeiten erarbeitet sich dann jedes Kind mit seiner eigenen Geschwindigkeit den nächsten Schwierigkeitsgrad. Da eine Fähigkeit jeweils mehrere Vorgänger- und Nachfolgerfähigkeiten hat, gibt es verschiedene Möglichkeiten für den nächsten Aufgabentyp bzw. für einfachere Aufgabenstellungen. Ein mathemathisches Modell im Hintergrund schätzt die Fähigkeiten ein und wählt entsprechend den nächsten Aufgabentyp. Auf diese Art und Weise ist der Spielablauf an das Kind angepasst und für jedes Kind verschieden.
Eine wichtige Eigenschaft ist der Einbau von Wiederholungen. Einfachere Fähigkeiten werden immer wieder repetiert, damit sie gefestigt werden. Da verschiedene Fähigkeiten durch verschiedene Aufgaben trainiert werden, erhöht diese Repetition zusätzlich auch die Variation der Aufgaben und damit die Flexibilität aber auch die Motivation. Die Repetitionen werden jeweils zufällig während des Trainings an einem Spiel eingestellt.
Darstellung der Zahlen
In allen Spielen, egal ob Haupt- oder Unterstützungsspiel wird eine einheitliche, konsistente Zahlendarstellung verwendet. Diese Zahlendarstellung betont gezielt die unterschiedlichen Repräsentationen von Zahlen. Verschiedene Eigenschaften von Zahlen werden dabei durch Farben, Formen sowie die Topologie codiert. Diese Codierung von Eigenschaften über verschiedene sensorische Merkmale erleichtert das Erlernen der Zahlenrepräsentationen und fördert das Zahlenverständnis.
Die Positionen des Dezimalsystems (1, 10, 100) werden durch Farben verschlüsselt. Dieser Effekt wird durch einen zusätzlichen Zahlengraph verstärkt (Abbildung 1). Jede einzelne Ziffer einer Zahl hängt an einem eigenen Ast dieses Zahlengraphs. Durch diese Repräsentation soll die Entwicklung der arabischen Notation sowie die Übersetzung zwischen Zahlwort und Arabischer Schreibweise gefördert werden.
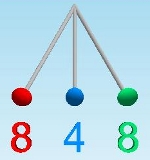
Abbildung 2: Repräsentation der Zahl 848 mit Farbe und Topologie.
Die Grösse einer Zahl wird auf zwei verschiedene Arten codiert. Die Zahl wird einerseits als Zusammensetzung von Blöcken verschiedener Farben, d.h., als eine Komposition von Einer-, Zehner- und Hunderterblöcken dargestellt (Abbildung 2). Diese Darstellung zeigt, dass eine Zahl immer als Zusammensetzung anderer Zahlen gesehen werden kann und betont das Dezimalsystem. Die Blöcke sind jeweils von links nach rechts angeordnet, um eine Verbindung zur räumlichen Zahlenrepräsentation (Zahlenstrahl) herzustellen. Eine zweite Codierung der Grösse erfolgt durch die Darstellung der Zahl direkt auf dem Zahlenstrahl. Die farbigen Blöcke werden dabei in den Zahlenstrahl integriert (Abbildung 3).
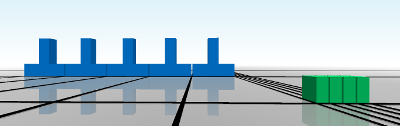
Abbildung 3: Repräsentation der Zahl 53 mit farbigen Blöcken in 3D.
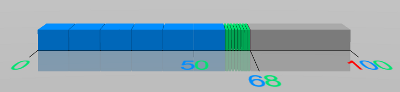
Abbildung 4: Räumliche Repräsentation der Zahl 68 auf dem Zahlenstrahl
Stand der Entwicklung
Calcularis befindet sich aktuell im Prototypenstadium und ist nur im Rahmen unserer Studien zugänglich.
Informationen zur Weiterentwicklung, allfälligen Probeversionen oder zu weiteren Resultaten der Studie können Sie über das Kontakformular anfordern.
Literatur
- Dehaene, S. (1992). Varieties of numerical abilities. Cognition, 44, 1-42.
- Kucian, K., Grond, U., Rotzer, S., Henzi, B., Schönmann, C., Plangger, F., Gälli, M., Martin, E. & von Aster M (2011). Mental mumber line training in children with developmental dyscalculia. NeuroImage, 57, 782-795.
- von Aster, M. G. & Shalev, R. S. (2007). Number development and developmental dyscalculia. Developmental Medicine & Child Neurology, 49, 868-673.
Zum Seitenanfang
|












