Modeling Engagement Dynamics in Spelling Learning
G.M. Baschera, A.G. Busetto, S. Klingler, J.M. Buhmann, M. GrossProceedings of AIED (Auckland, New Zealand, June 28 - July 2, 2011), pp. 31-38
Abstract
In this paper, we introduce a model of engagement dynamics in spelling learning. The model relates input behavior to learning, and explains the dynamics of engagement states. By systematically incorporating domain knowledge in the preprocessing of the extracted input behavior, the predictive power of the features is significantly increased. The model structure is the dynamic Bayesian network inferred from student input data: an extensive dataset with more than 150 000 complete inputs recorded through a training software for spelling. By quantitatively relating input behavior and learning, our model enables a prediction of focused and receptive states, as well as of forgetting.Overview
Due to its recognized relevance in learning, affective modeling is receiving increased attention. Models of affect are developed based on experimental readouts, which are assumed to be related to affect. However, there are two reasons why modeling affect is considered a particularly challenging task. First, ground truth is invariably approximated. Second, experimental readouts and state emissions often exhibit partial observability and significant noise levels. The latter is caused by the fact that observed student input behavior, e.g., the student input rate, is not influenced by affective states only. Various social, environmental and task dependent influences act simultaneously on the observed feature. Additionally, the input behavior is often subject to progress over time. The two main difficulties in affective modeling are:
- Non-i.i.d. data: Due to the progress in typing the extracted data is not independent and identically distributed. However, this property is required for statistical inference.
- Scaling: The exact specification of the observed behavior and its scaling will strongly influences the predictive power of a feature.
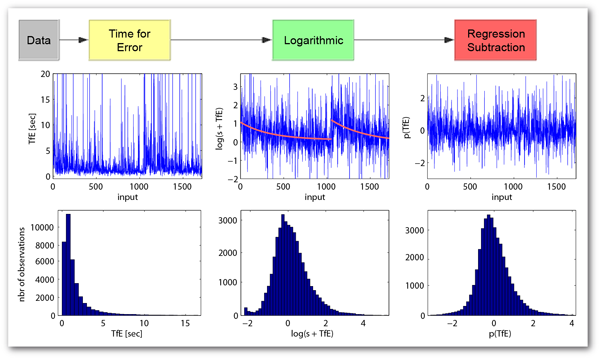
We develop a model of engagement dynamics in spelling learning by quantitatively relating input behavior to learning. The method for feature processing in affective modeling is employed to increase the predictive power of the observed input behavior.
Results
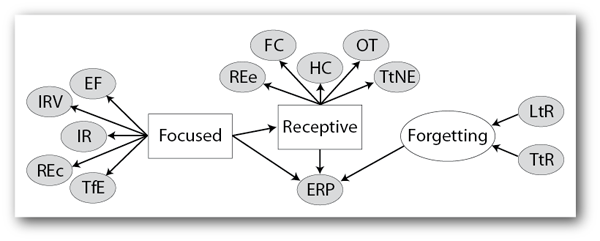
In this publication we describe the development of a model of engagement dynamics. The model is based on features extracted from the input data collected in the first user study. A regression analysis demonstrates that the systematic approach to feature processing for affective modeling increases the predictive power of the employed features. Especially all timing features benefited strongly from the appropriate scaling. The structure of the dynamic Bayesian network was identified on the basis of input and error behaviors alone. The model jointly represents the influences of Focused and Receptive states on learning, as well as the decay of spelling knowledge due to Forgetting. The presented causal model can be investigated and exhibits coherent conclusions.
This core model can be extended with assessments of engagement of a different nature, such as sensor, camera or questionnaire data. This would allow to verify the annotation of the hidden nodes and to relate the identified states to the underlying fundamental affective dimensions.