Evaluation and FPGA Implementation of Sparse Linear Solvers for Video Technology
P. Greisen, M. Runo, P. Guillet, S. Heinzle, A. Smolic, H. Kaeslin, M. GrossIEEE Transactions on Circuits and Systems for Video Technology, 2013
Abstract
Sparse linear systems are commonly used in video processing applications, such as edge-aware filtering or video retargeting. Due to the 2D nature of images, the involved problem sizes are large and thus solving such systems is computationally challenging. In this work, we address sparse linear solvers for real-time video applications. We investigate several solver techniques, discuss hardware trade-offs, and provide FPGA architectures and implementation results of a Cholesky direct solver and of an iterative BiCGSTAB solver. The FPGA implementations solve 32K x 32K matrices at up to 50 fps and outperform software implementations by at least one order of magnitude.Overview
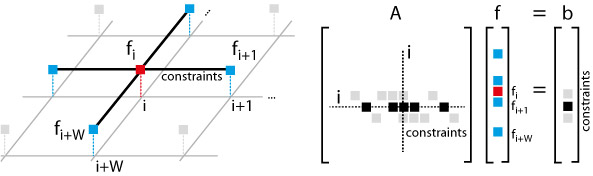
Although a multitude of algorithms for solving general linear systems have been reported, the application to real-time video processing has not been addressed thoroughly. The main difficulty lies in the involved problem size, resulting in a huge number of floating-point operations (FLOPs), as well as in huge memory and bandwidth requirements. While these linear systems can often be solved on lower resolution discretization grids without noticeable quality loss, the current trend towards ever higher frame-rates and image resolutions poses significant challenges on solving such systems in real-time. In this work, we address FPGA architectures of sparse linear systems for computer vision and video processing. Common solver techniques are revisited regarding computational efficiency at the example of image domain warping (IDW) applications such as aspect ratio retargeting or stereo-to-multiview conversion. To achieve high computational power, we design custom FPGA architectures for an iterative solver (bi-conjugate gradient stabilized (BiCGSTAB)) and a direct solver (CHOLESKY). We compare the two FPGA implementation results and discuss the general trade-offs of iterative and direct solvers on FPGAs in terms of hardware resources, memory bandwidth, and on-chip storage requirements. Furthermore, we compare our FPGA implementations to software implementations. In contrast to programmable hardware (CPUs, GPUs), our dedicated hardware architectures are more energy-efficient and can achieve very high resource utilization, since the hardware resources can be matched to the specific algorithm.
Results
Linear solvers for video processing are computationally demanding. The use of dedicated hardware offers at least one order of magnitude speed-up against modern CPU-based computing platforms. More importantly, dedicated solver hardware can be integrated into next generation mobile devices, due to their high energy efficiency (performance per Watt). The use of direct or iterative solver depends on the available hardware resources and the application: iterative solvers require a lot of memory bandwidth and benefit from strong correlations among frames; direct solvers are computation limited and cannot use previous frames to speed-up calculations. A very interesting direction for future work is to investigate recent and upcoming graph-theory based pre-conditioner approaches for dedicated hardware.