Generic Objective Vortices for Flow Visualization
T. Günther, M. Gross, H. TheiselProceedings of ACM SIGGRAPH (Los Angeles, USA, July 30 - August 3, 2017), ACM Transactions on Graphics, vol. 36, no. 4, pp. 141:1--141:11
Abstract
In flow visualization, vortex extraction is a long-standing and unsolved problem. For decades, scientists developed numerous definitions that characterize vortex regions and their corelines in different ways, but none emerged as ultimate solution. One reason is that almost all techniques have a fundamental weakness: they are not invariant under changes of the reference frame, i.e., they are not objective. This has two severe implications: First, the result depends on the movement of the observer, and second, they cannot track vortices that are moving on arbitrary paths, which limits their reliability and usefulness in practice. Objective measures are rare, but recently gained more attention in the literature. Instead of only introducing a new objective measure, we show in this paper how all existing measures that are based on velocity and its derivatives can be made objective. We achieve this by observing the vector field in optimal local reference frames, in which the temporal derivative of the flow vanishes, i.e., reference frames in which the flow appears steady. The central contribution of our paper is to show that these optimal local reference frames can be found by a simple and elegant linear optimization. We prove that in the optimal frame, all local vortex extraction methods that are based on velocity and its derivatives become objective. We demonstrate our approach with objective counterparts to lambda2, vorticity and Sujudi-Haimes.Overview
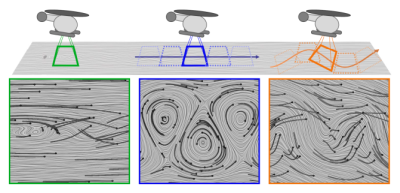
Vortices are omnipresent features. Even though they have been studied for centuries, there is still no commonly agreed upon definition of what a vortex is. Most existing vortex concepts have a fundamental weakness: they are not invariant under changes of the reference frame. To illustrate this, consider the following example:
We see a simple 2D flow, e.g., a river. A person observing the flow from a helicopter that stands still (left) observes a different flow than a person in a helicopter that moves with constant speed (middle) or along an arbitrary path (right). A vortex measure that finds the same structures in every rotating or translating reference frame is called objective.
Results
We propose a generic method that transforms almost every existing vortex measure into an objective one. The main idea is to compute a local optimal reference frame in which the flow appears as steady as possible in a small region around the point of interest. After showing that the locally optimal frame can be computed by a simple linear optimization at every point, we obtain new objective versions of the velocity, Jacobian and acceleration fields. Then, an existing vortex measure can be made objective simply by replacing the original fields with their objective counterparts.
Code
A VTK filter for our optimal local reference frames is available on GitHub for unsteady 2D vector fields.