Modelling and Optimizing the Process of Learning Mathematics
T. Käser, A.G. Busetto, G.M. Baschera, J. Kohn, K. Kucian, M. von Aster, M. GrossIntelligent Tutoring Systems (Chania, Greece, June 14-18, 2012), pp. 389-398
Abstract
This paper introduces a computer-based training program for enhancing numerical cognition aimed at children with developmental dyscalculia. Through modelling cognitive processes and controlling the level of their stimulation, the system optimizes the learning process. Domain knowledge is represented with a dynamic Bayesian network on which the mechanism of automatic control operates. Accumulated knowledge is estimated to select informative tasks and to evaluate student actions. This adaptive training environment equally improves success and motivation. Large-scale experimental data quantifies substantial improvement and validates the advantages of the optimized training.Overview
Computer-assisted learning is gaining importance in children's education. Intelligent tutoring systems are successfully employed in different fields of education, particularly also to overcome learning disabilities. Developmental dyscalculia (DD) is a specific learning disability affecting the acquisition of arithmetic skills. Challenges are subject-dependent and hence individualization is needed to achieve substantial improvements. Computer-based approaches enable the design of adaptable training, by estimating abilities and by providing intensive training in a stimulating
environment.
In this publication, we present a computer-based training environment for children with DD or difficulties in learning mathematics, along with a model for the mathematical abilities of the children. We base the content of the training program on neuropsychological findings. The structure and games of the training program are aligned to the natural development of number understanding in children. We introduce a highly specific design for numerical stimuli enhancing the different number representations and facilitating number understanding (Fig. 1).
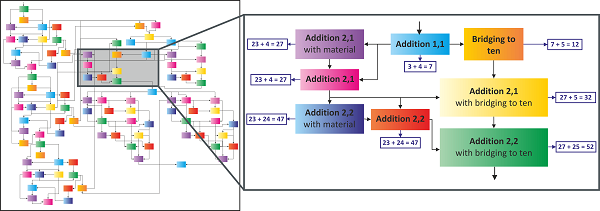
The training program features a pedagogical module selecting the skills and determining the actions.The mechanisms adaptively assess user inputs and dynamically optimize decisions. The learner state is estimated and internally represented by the student model. The mathematical knowledge of the learner is modelled using a dynamic Bayesian network. The network consists of a directed acyclic graphical model representing different mathematical skills and their dependencies. The resulting model contains 100 different skills (Fig. 2).
The selection of actions is rule-based and non-linear. Rather than following a specified sequence to the goal, learning paths are adapted individually. Especially, knowledge gaps and forgetting are implicitly modelled by the possibility to go back to consolidate an easier skill.
Results
To assess the quality of the controller and the student model, we used external effectiveness measures as well as input logs. The data stem from two on-going user studies in Germany and Switzerland.
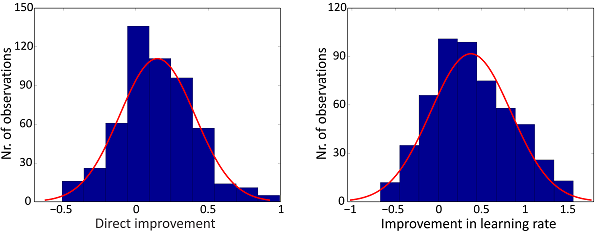
Analyses of the input data show, that the participants improved over time. They provide evidence that the introduced control mechanism significantly speeds up the learning process and that it rapidly adapts to the individual user. We especially demonstrate that the possibility to go back to easier (played or unplayed) skills yields a substantially beneficial effect. The user not only immediately starts reducing the rate of mistakes, but also learns faster (Fig. 3).
The external effectiveness tests showed significant improvements in subtraction tasks. The focus on subtraction and the significant improvement coming with it is scientifically interesting as performance in subtraction is considered the main indicator for numerical understanding. Consistently with this, improved number line representation was directly measurable from the input data.