Cluster-Based Prediction of Mathematical Learning Patterns
T. Käser, A.G. Busetto, B. Solenthaler, J. Kohn, M. von Aster, M. Gross16th International Conference, AIED 2013 (Memphis, USA, 9-13 July 2013)
Abstract
This paper introduces a method to predict and analyse students' mathematical performance by detecting distinguishable subgroups of children who share similar learning patterns. We employ pairwise clustering to analyse a comprehensive dataset of user interactions obtained from a computer-based training system. The available data consist of multiple learning trajectories measured from children with developmental dyscalculia, as well as from control children. Our online classification algorithm allows accurate assignment of children to clusters early in the training, enabling prediction of learning characteristics. The included results demonstrate the high predictive power of assignments of children to subgroups, and the significant improvement in prediction accuracy for short- and long-term performance, knowledge gaps, overall training achievements, and scores of further external assessments.Overview
Computer-assisted learning has entered different fields of education. Computer-based therapy systems for learning disabilities have gained particular attention. Such systems present inexpensive extensions to conventional one-toone therapy by providing an adaptive and fear-free learning environment. To improve diagnostics and intervention outcomes, knowledge of performance profile, knowledge gaps and learning behaviours of the student as well as an accurate performance prediction are essential. This is particularly important for students suffering from learning disabilities as the heterogeneity of these children requires a high grade of individualization.
The present study aims at predicting and analysing children's mathematical performance on the basis of distinguishable learning patterns extracted from similar subgroups of students. Our approach is articulated in two steps. Firstly, we cluster children after the complete training to identify subgroups with similar mathematical learning patterns. Secondly, we classify children to a particular subgroup after each training session to predict future performance. Whereas existing contributions address the task of predicting short-term performance and external assessment results, we introduce a method which also predicts learning characteristics such as knowledge gaps and overall training achievement.
Results
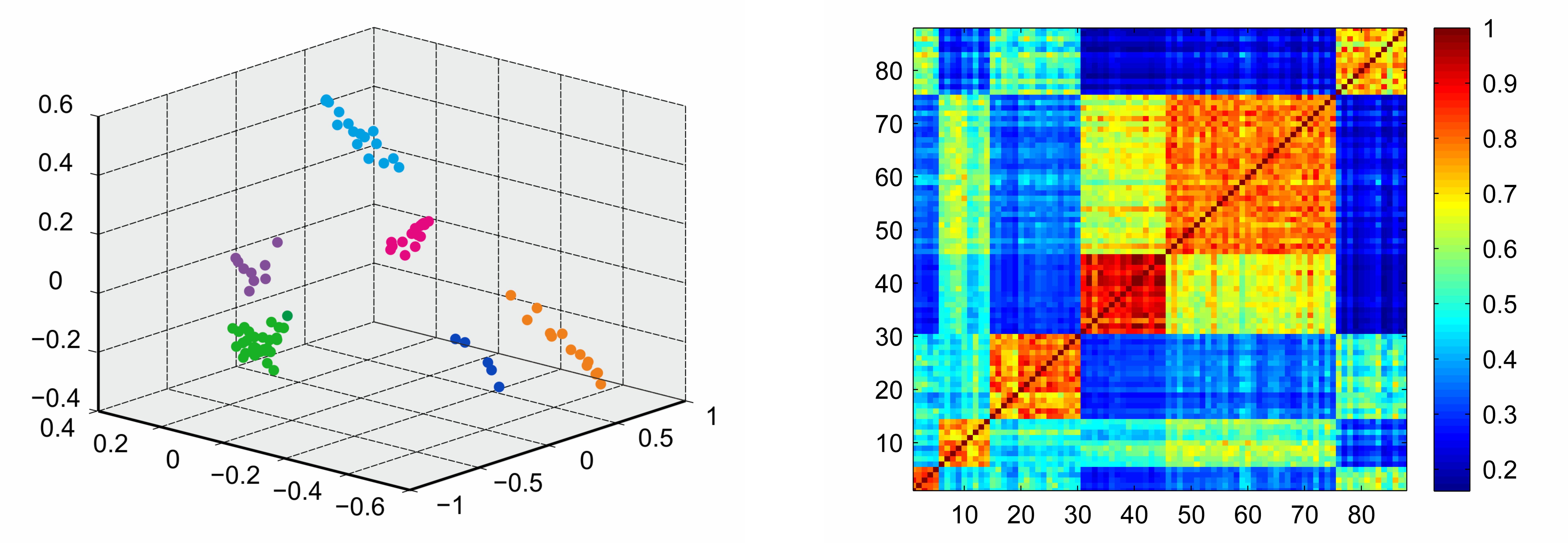
Computation of the BIC suggests that dividing the children into k=6 subgroups is optimal. This result is supported by the clear separability of the transformed data in three dimensions (Fig. 1, left) and the clearly visible clusters on the diagonal of the similarity matrix (Fig. 1, right). Furthermore, the six clusters can be interpreted regarding the characteristics of distinct learning patterns of the children.
During training, we classify the children to a particular subgroup depending on their current training status. As expected, classification accuracy increases with the number of training sessions. Five sessions are already sufficient for our method to cluster 50% of the children correctly. Prediction of students' performance is significantly reduced when taking cluster information into account. A good prediction accuracy is reached already after few trainings and allows to draw conclusions about short-term performance and knowledge gaps.
The results demonstrate that the prediction accuracy can be significantly increased by taking subgroup information into account. The usefulness of clustering for the analysis of learning pattern and further training individualization contribute to a better support for children with learning difficulties.