Design and evaluation of the computer-based training program Calcularis for enhancing numerical cognition
T. Käser, G. M. Baschera, J. Kohn, K. Kucian, V. Richtmann, U. Grond, M. Gross, M. von AsterFrontiers in Developmental Psychology, 4:289, 2013
Abstract
This article presents the design and a first pilot evaluation of the computer-based training program Calcularis for children with developmental dyscalculia (DD) or difficulties in learningmathematics. The program has been designed according to insights on the typical and atypical development of mathematical abilities. The learning process is supported through multimodal cues, which encode different properties of numbers. To offer optimal learning conditions, a user model completes the program and allows flexible adaptation to a child’s individual learning and knowledge profile. 32 children with difficulties in learning mathematics completed the 6–12-weeks computer training. The children played the game for 20 min per day for 5 days a week. The training effects were evaluated using neuropsychological tests. Generally, children benefited significantly from the training regarding number representation and arithmetic operations. Furthermore, children liked to play with the program and reported that the training improved their mathematical abilities.Overview
Arithmetical skills are essential inmodern society.However, many children experience difficulties in learning mathematics, ranging from mild to severe numeracy problems. So far, only few studies have investigated targeted interventions based on neuro-cognitive findings of the typical and atypical development of mathematical abilities. Only a fraction of these are computer-based. Existing training programs have demonstrated the efficacy of computer-based intervention in number processing. These interventions however mostly focus on specific skills (such as the training of fact knowledge) and provide only limited adaptability.
In this study, we describe the development of a computer-based intervention targeting children with difficulties in learning mathematics along with a first evaluation. The training program combines the training of basic numerical cognition with the training of arithmetic abilities. The learning process is supported through multimodal cues, which encode different properties of numbers. To offer optimal learning conditions, a user model completes the program and allows flexible adaptation to a child’s individual learning and knowledge profile
Training program
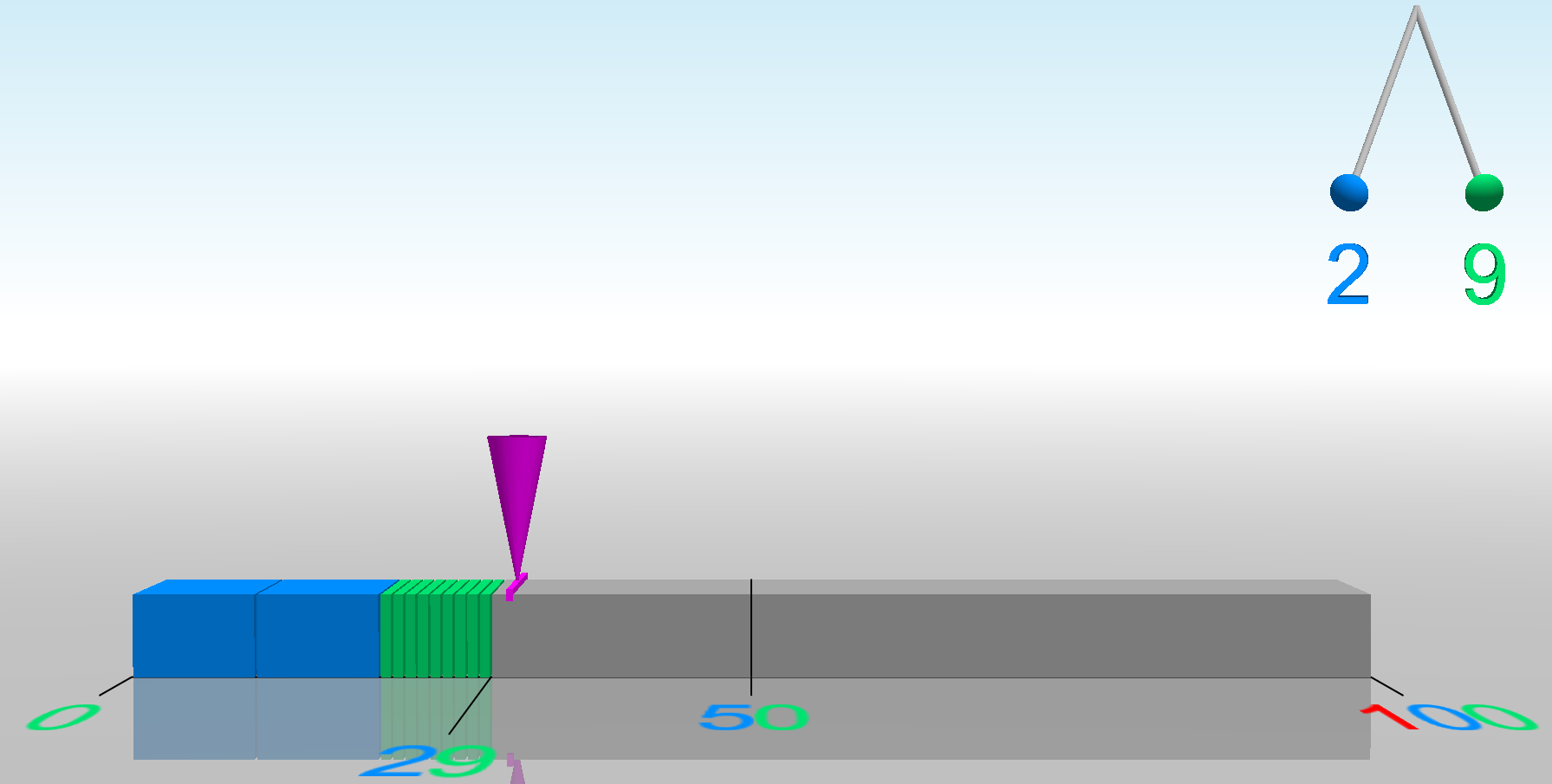
The training program is composed of multiple games in a hierarchical structure. Games are structured according to number ranges and further grouped into two areas. The first area focuses on “number representations and understanding”. It trains the transcoding between alternative representations and introduces the three principles of number understanding: cardinality, ordinality, and relativity. Games in this area are structured according to current neuropsychological models. This area is exemplified by the landing game (Fig. 1). The second area is that of “cognitive operations and procedures with numbers”, which aims at training concepts and automation of arithmetical operations. The different games are categorized according to their complexity and relative importance. Main games require a combination of abilities to solve them, while support games train specific skills and serve as basic prerequisites. Difficulty estimation and hierarchy result from the development of mathematical abilities.
The intervention also features a secial design for numerical stimuli to to enhance the different number modalities and to strengthen the links between them. Properties of numbers are encoded with visual cues such as color, form and topology.
Furthermore, the learning process of children is optimized by providing a hierarchically structured learning environment teaching fundamental knowledge first (scaffolding). Furthermore, it is fully adaptive to customize the learning experience of the child. Task difficulty is adapted to the child and specific problems of a child are recognized and addressed. The student model used is a dynamic Bayesian network consisting of 100 different mathematical skills and the dependencies among them (an extract of the network is displayed in figure 3). A controller acts on this network and selects the skills for training based on the posterior probabilites of the Bayesian network.
Results
The effects of the training program have been assessed in a study with 41 children conducted in Switzerland. Participants were divided into a training group (n = 20, 65% females) completing a 12-weeks training and a waiting group (n = 21, 66.6% females) starting with a 6-weeks rest period. Mathematical performance of both groups was evaluated at the beginning of the study (t1), after 6 weeks (t2) and after 12 weeks (t3). Children were required to train with the program 5 times per week, with daily training sessions of 20min.
Our first results reveal positive training effects in mathematical skills after completion of the training. Children improved significantly in subtraction and spatial number representation after 6 weeks of training. For most of the tasks tested tested before and after training, prolongation of the training from 6 to 12 weeks yielded a beneficial effect.
Feedback from children who have completed the training and rated the difficulty level of the learning program as appropriate, confirms that the quality of the adaptation and the estimation of the children’s knowledge were sufficient. On average, children reported that the training had improved their mathematical performance. Moreover, children also indicated that they liked to train with the program. The popularity of the learning environment is beneficial as training can only be successful if the children are motivated.