Modelling and Optimizing Mathematics Learning in Children
T. Käser, A. G. Busetto, B. Solenthaler, G.-M. Baschera, J. Kohn, K. Kucian, M. von Aster, M. GrossIJAIED: "Best of ITS 2012", , vol. 23, no. 1-4, 2013, pp. 115-135
Abstract
This study introduces a student model and control algorithm, optimizing mathematics learning in children. The adaptive system is integrated into a computer-based training system for enhancing numerical cognition aimed at children with developmental dyscalculia or difficulties in learning mathematics. The student model consists of a dynamic Bayesian network which incorporates domain knowledge and enables the operation of an online system of automatic control. The system identifies appropriate tasks and exercise interventions on the basis of estimated levels of accumulated knowledge. Student actions are evaluated and monitored to extract statistical patterns which are useful for predictive control. The training system is adaptive and personalizes the learning experience, which improves both success and motivation. Comprehensive testing of input data validates the quality of the obtained results and confirms the advantage of the optimized training. Pilot results of training effects are included and discussed.Overview
Arithmetic skills are important in modern society, as numerical cognition and calculations are omnipresent in everyday life. However, many children suffer from difficulties in learning mathematics. Developmental dyscalculia (DD) is a specific learning disability affecting the acquisition of arithmetic skills. DD has an estimated prevalence of 3-6% in English- and German-speaking countries. The relatively high prevalence of DD suggests that it is important to investigate intervention approaches to prevent or remediate learning difficulties in mathematics. Existing computer-based training programs are carefully designed for children with difficulties in
learning mathematics, however, they lack user adaptation.
The present work is based on the intelligent tutoring system ’Calcularis’ (Käser et al., 2012). In this system, we model the cognitive processes of mathematical development using a dynamic Bayesian network. Our student model represents different mathematical skills and their dependencies. An automatic control mechanism aimed at optimizing learning and acting on the skill net is introduced. The design of the skill net allows for a non-linear control mechanism. In contrast to previous approaches, we allow movements along all edges of the skill net (particularly also backward movements), which enables us to implicitly model forgetting and knowledge gaps. The model’s predictive control enables a significant level of cognitive stimulation which is user- and context-adaptive. We assess the efficiency and adaptability of the introduced student model and control mechanism based on input logs from two user studies in Germany and Switzerland. Furthermore, we analyse properties of users and skills used in the model. Finally, we also include first pilot results of the obtained training effects.
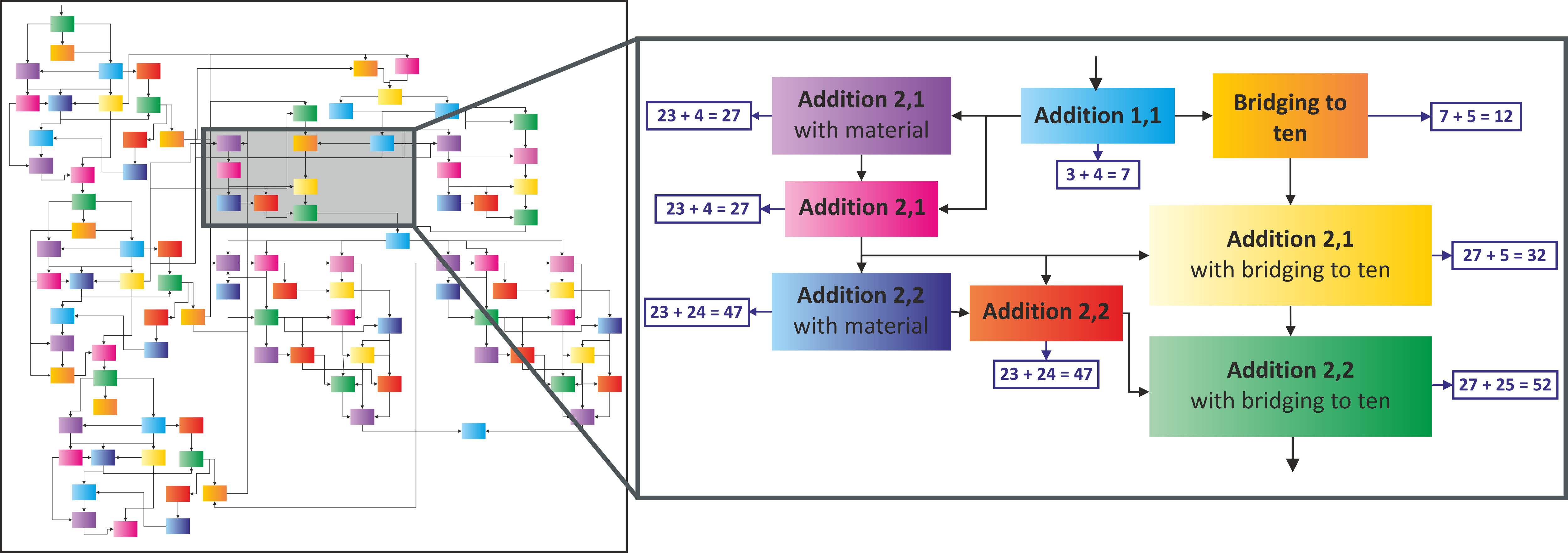
Student model and control
The mathematical knowledge of the learner is modelled using a dynamic Bayesian network. The network consists of a directed acyclic graphical model representing different mathematical skills and their dependencies. As the skills cannot be directly observed, the system infers them by posing tasks and evaluating user actions. The posteriors of the net are updated after each solved task. The skill net representation is ideal for modelling mathematical knowledge as the learning domain exhibits a distinctively hierarchical structure. Our resulting student model contains 100 different skills as illustrated in Fig. 1
Due to the design of the student model, the selection of actions is rule-based an non-linear. Rather than following a specified sequence to the goal, learning paths are adapted individually. This increases the set of possible actions (due to multiple precursor and successor skills). To pick the optimal precursor/successor skill, the controller therefore follows a set of priority rules encoded in a decision tree.Results
Experimental data consisted of input logs recorded from 63 participants and containing six weeks of training.On average, each user completed 29.77 (SD 2.43, min 24, max 36) sessions. To measure the improvement of participants over the course of the training, we introduced the concept of key skills. Key skills are defined in terms of subject-dependent difficulty, they are the hardest skills for the user to pass. A non-linear mixed effect model using a log link demonstrates a mean improvement of 21.8% over the course of the training. Children also improved in external arithmetic tests. We found significant improvement in subtraction and subtraction speed.
Further analysis demonstrates that the possibility to go back to easier (played or unplayed) skills yields a significant beneficial effect. The user not only immediately starts reducing the rate of mistakes, but also learns faster.