Beyond Knowledge Tracing: Modeling Skill Topologies with Bayesian Networks
T. Käser, S. Klingler, A. G. Schwing, M. GrossProceedings of ITS (Honolulu, Hawaii, June 5-9, 2014), pp. 188-198
Abstract
Modeling and predicting student knowledge is a fundamental task of an intelligent tutoring system. A popular approach for student modeling is Bayesian Knowledge Tracing (BKT). BKT models, however, lack the ability to describe the hierarchy and relationships between the different skills of a learning domain. In this work, we therefore aim at increasing the representational power of the student model by employing dynamic Bayesian networks that are able to represent such skill topologies. To ensure model interpretability, we constrain the parameter space. We evaluate the performance of our models on five large-scale data sets of different learning domains such as mathematics, spelling learning and physics, and demonstrate that our approach outperforms BKT in prediction accuracy on unseen data across all learning domains.Overview
Intelligent tutoring systems (ITS) are successfully employed in different fields of education. A key feature of these systems is the adaptation of the learning content and the difficulty level to the individual student. The selection of problems is based on the estimation and prediction of the studentís knowledge by the student model. Therefore, modeling and predicting student knowledge accurately is a fundamental task of an intelligent tutoring system.
One of the most popular approaches to assess and predict student performance is Bayesian Knowledge Tracing (BKT). As the prediction accuracy of a probabilistic model is dependent on its parameters, an important task when using BKT is parameter learning. Exhibiting a tree structure, BKT allows for efficient parameter learning and accurate inference. However, tree-like models lack the ability to represent the hierarchy and relationships between the different skills of a learning domain. Employing dynamic Bayesian network models (DBN) has the potential to increase the representational power of the student model and hence further improve prediction accuracy. Despite their beneficial properties to represent knowledge, DBNs have received less attention in student modeling as they impose challenges for learning and inference.
In this paper, we propose the the use of DBNs to model skill hierarchies within a learning domain. We use a log-linear formulation and apply a constrained optimization to identify the parameters of the DBN. We define domain-specific DBN models for five large-scale data sets from different learning domains, containing up to 7000 students. Studentsí age ranges from elementary school to university level. Our results show that even simple skill hierarchies lead to significant improvements in prediction accuracy of up to 10% over BKT across all learning domains. By using the same constraints and parameterizations for all experiments, we also demonstrate that basic assumptions about learning hold across different learning domains and thus our approach is easy to use.
Results
We show the benefits of DBN models with higher representational power on five data sets from various learning domains. The data sets were collected with different tutoring systems and contain data from elementary school students up to university students. We compare the prediction accuracy of DBNs modeling skill topologies with the performance of traditional BKT models.
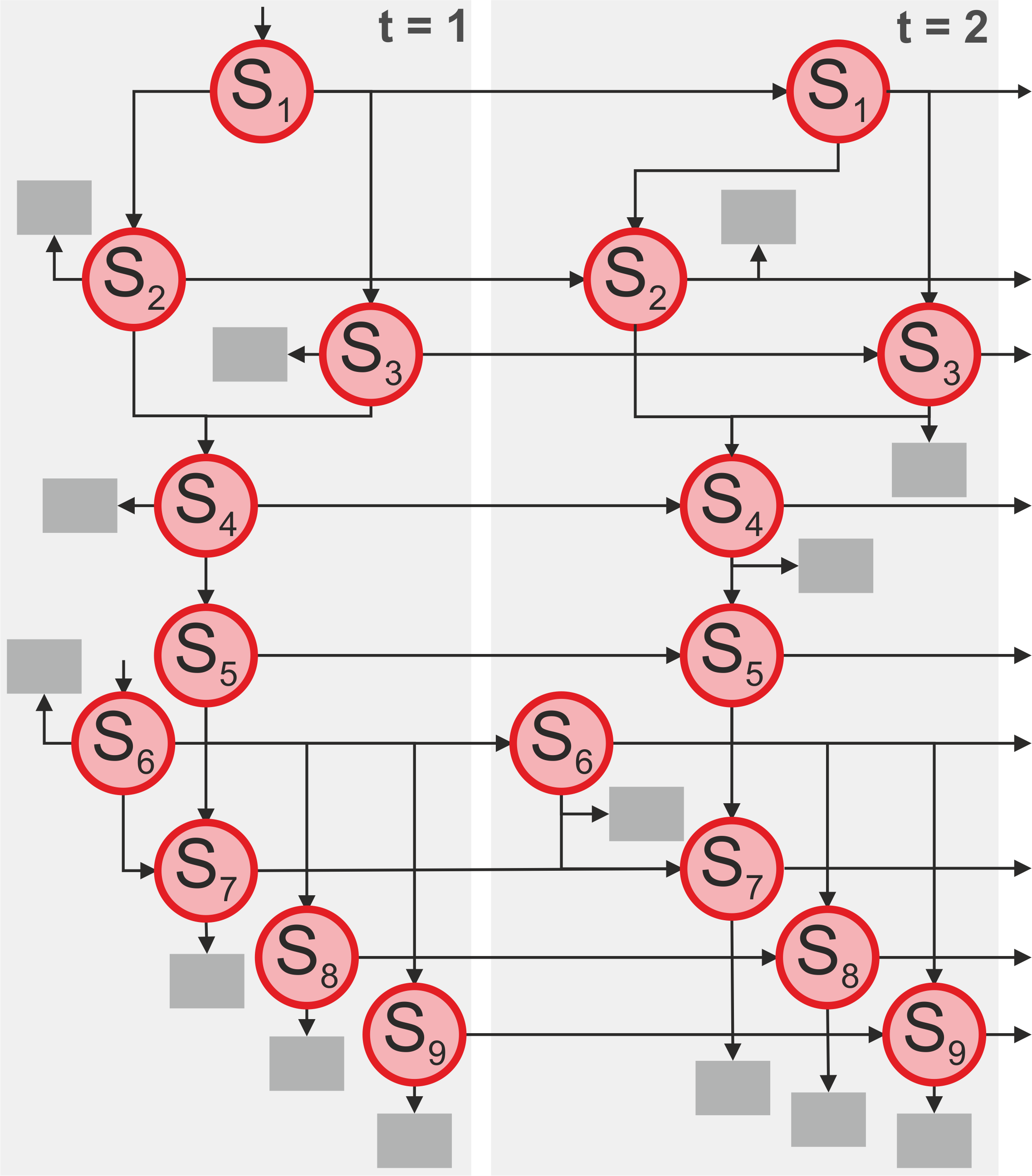
In one experiment, we use data collected from an intelligent tutoring system for elementary school children with math learning difficulties. The data set contains log files of 1581 children with at least 5 sessions of 20 minutes per user. The program represents student knowledge as a DBN consisting of different mathematical skills. The graphical model used in this experiment is illustrated in Fig. 1. The skills represent subtraction tasks at different difficulty levels. Applying a DBN instead of BKT for this experiments leads to an improvement of 3.5% in root mean squared error (RMSE), an increase of 8.4% in accuracy and a substantial growth of the area under curve (AUC). The details of the experiments on the four other data sets can be found in the paper.
The results of the experiments demonstrate that more complex DBN models outperform BKT in prediction accuracy. For hierarchical learning domains, CE can be reduced by 10%, while improvements of RMSE by 5% are feasible. The DBN models generally exhibit a significantly higher AUC than BKT, which indicates that they are better at discriminating failures from successes. As expected, adding skill topologies has a much smaller benefit for learning domains that are less hierarchical in nature (such as spelling learning). The results obtained on the physics and algebra data sets show that even simple hierarchical models improve prediction accuracy significantly. A domain expert employing a more detailed skill topology and more complex constraint sets could probably obtain an even higher accuracy on these data sets. The use of the same parameterization and constraint sets for all experiments demonstrates that basic assumptions about learning hold across different learning domains and thus the approach is easy to use.