Multi-Perspective Stereoscopy from Light Fields
C. Kim, A. Hornung, S. Heinzle, W. Matusik, M. GrossProceedings of ACM SIGGRAPH Asia (Hong Kong, China, December 12-15, 2011), ACM Transactions on Graphics, vol. 30, no. 6, pp. 190:1-190:10
Abstract
This paper addresses stereoscopic view generation from a light field. We present a framework that allows for the generation of stereoscopic image pairs with per-pixel control over disparity, based on multi-perspective imaging from light fields. The proposed framework is novel and useful for stereoscopic image processing and post-production. The stereoscopic images are computed as piecewise continuous cuts through a light field, minimizing an energy reflecting prescribed parameters such as depth budget, maximum disparity gradient, desired stereoscopic baseline, and so on. As demonstrated in our results, this technique can be used for efficient and flexible stereoscopic post-processing, such as reducing excessive disparity while preserving perceived depth, or retargeting of already captured scenes to various view settings. Moreover, we generalize our method to multiple cuts, which is highly useful for content creation in the context of multi-view autostereoscopic displays. We present several results on computer-generated content as well as live-action content.Overview
Three-dimensional stereoscopic television, movies, and games have been gaining more and more popularity both within the entertainment industry and among consumers. An ever increasing amount of content is being created, distribution channels including live-broadcast are being developed, and stereoscopic monitors and TV sets are being sold in all major electronic stores. However, the task of creating convincing yet perceptually pleasing stereoscopic content remains difficult. This is mainly because post-processing tools for stereo are still underdeveloped, and one often has to resort to traditional monoscopic tools and workflows, which are generally ill-suited for stereo-specific issues. This situation creates an opportunity to rethink the whole post-processing pipeline for stereoscopic content creation and editing.
The main cue responsible for stereoscopic scene perception is binocular parallax (or binocular disparity) and therefore tools for its manipulation are extremely important. One of the most common methods for controlling the amount of binocular parallax is based on setting the baseline, or the inter-axial distance, of two cameras prior to acquisition. However, the range of admissible baselines is quite limited since most scenes exhibit more disparity than humans can tolerate when viewing the content on a stereoscopic display. Reducing baseline decreases the amount of binocular disparity; but it also causes scene elements to be overly flat. The second, more sophisticated approach to disparity control requires remapping image disparities (or remapping the depth of scene elements), and then re-synthesizing new images. This approach has considerable disadvantages as well; for content captured with stereoscopic camera rigs, it typically requires accurate disparity computation and hole filling of scene elements that become visible in the re-synthesized views. For computer-generated images, changing the depth of the underlying scene elements is generally not an option, because changing the 3D geometry compromises the scene composition, lighting calculations, visual effects, etc.
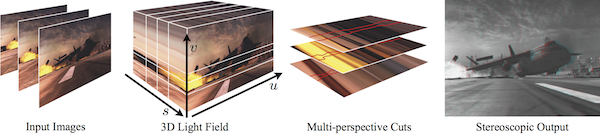
In this paper we propose a novel concept for stereoscopic post-production to resolve these issues. The main contribution is a framework for creating stereoscopic images, with accurate and flexible control over the resulting image disparities. Our framework is based on the concept of 3D light fields, assembled from a dense set of perspective images. While each perspective image corresponds to a planar cut through a light field, our approach defines each stereoscopic image pair as general cuts through this data structure, i.e. each image is assembled from potentially many perspective images. We show how such multi-perspective cuts can be employed to compute stereoscopic output images that satisfy an arbitrary set of goal disparities. These goal disparities can be defined either automatically by a disparity remapping operator or manually by the user for artistic control and effects. The actual multi-perspective cuts are computed on a light field, using energy minimization based on graph-cut optimization to compute each multi-perspective output image. We also present a number of extensions for this basic framework, including a method to drive multi-view autostereoscopic displays more flexibly and efficiently by computing multiple cuts through a light field.
Results
In our results we present a number of different operators including global linear and nonlinear operators, but also local operators based on nonlinear disparity gradient compression. Here, we present a few of those results: see the paper and video for more.
Figure 2 demonstrates the use of nonlinear disparity remapping function in conjunction with our framework. The top-left image (a) shows a standard stereo pair with a large baseline where the foreground provides a good impression of depth. The background disparities, however, are quite large and can lead to ghosting artifacts or even the inability to fuse, when viewed on a larger screen. Decreasing the baseline reduces the problems with respect to the background, but also considerably reduces the depth between the foreground and the background as shown in (b). In the image (c), with a nonlinear disparity mapping function we enhance the depth impression of the foreground, while keeping the maximum disparities in the background bounded as in the image (b). Compare the disparity distribution (h) to that of the small baseline stereo (f). (d), (f), and (h) show the disparity distributions of respective stereo pairs, and (e) and (g) show the disparity remapping functions. Observe that the depth between the foreground and the background in (d) is preserved in (h), while it is not in (f).
Figure 3 shows more examples, where nonlinear disparity gradient remapping was applied in order to reduce the overall disparity range, while preserving the perception of depth discontinuities and local depth variations. The first row shows the stereo pairs with two perspective images and a fixed baseline, while the second row shows the depth remapped versions. In particular, for the airplane scene (the third and fourth columns) the disparity gradient of the image's upper half was intensified, and the gradient of the lower half was attenuated. See the video for the full sequences.