Unified Simulation of Elastic Rods, Shells, and Solids
S. Martin, P. Kaufmann, M. Botsch, E. Grinspun, M. GrossProceedings of ACM SIGGRAPH (Los Angeles, USA, July 25-29, 2010), ACM Transactions on Graphics, vol. 29, no. 3, pp. 39:1-39:10
Abstract
We develop an accurate, unified treatment of elastica. Following the method of resultant-based formulation to its logical extreme, we derive a higher-order integration rule, or elaston, measuring stretching, shearing, bending, and twisting along any axis. The theory and accompanying implementation do not distinguish between forms of different dimension (solids, shells, rods), nor between manifold regions and non-manifold junctions. Consequently, a single code accurately models a diverse range of elastoplastic behaviors, including buckling, writhing, cutting and merging. Emphasis on convergence to the continuum sets us apart from early unification efforts.Overview
Elastic bodies take many forms, from long and slender rods, to flat and wide shells, to thick and bulky solids. Over the past decades specialized methods have emerged for the efficient and compelling simulation of each of these forms. But this specialization has opened a Pandora’s box: we must debug, extend, and interface between multiple specialized codes. We struggle both with the software interface as well as with the mathematical, or physical model of the interface. And how do we model the physics of objects that do not neatly fit into one of the categories? Junctions, for example, are outside the scope of most specialized models, and are treated as an afterthought.
Some shapes transition smoothly (either along their spatial dimension, or as they evolve temporally) between one form and another - must we make a binary decision in categorizing them? If two specialized methods use a different geometric representation (points, triangles, tetrahedra), the question of how to transition is doubly complicated. We argue that a simple, unified treatment spanning rods, shells, and solids is possible and desirable. By unified, we mean that the code does not distinguish between forms. We draw motivation from previous unification efforts, but are set apart by our emphasis on physical correctness, specifically convergence to the continuum model.
Results
We also verified the qualitative behavior of our model on a couple of well-known test cases for shells and rods. Figure 2 shows a thin cylinder that develops the expected buckling patterns as it is compressed, and demonstrates that we are able to reproduce the characteristic dynamic behavior of rods, building plectonemes and helical perversions as shown in previous publications on rods.
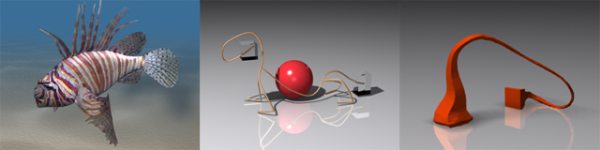
Real-world objects often consist of complex assemblies of different forms of geometry. Our method is able to handle these mixed cases in a unified manner as demonstrated in Figure 3. These examples would be difficult to realize by combining several specialized methods.
Objects can not only transition between solid, shell, and rod in space, regime changes can also develop over time. In plastic and viscous deformations, for instance, material can be stretched into thin sheets or strands (Figure 4), whose elastic behavior can correctly be captured by our approach.
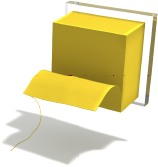
Thin structures can also show up dynamically due to cutting or fracturing. We handle cutting by adapting the idea of a connectivity graph and the virtual node approach. Figure 5 shows a block of material being cut twice into a very thin slice and rod. Our renderer likewise cuts the embedded triangle mesh.