Spectral Sampling of Manifolds
C. Öztireli, M. Alexa, M. GrossProceedings of ACM SIGGRAPH Asia (Seoul, Korea, December 15-18, 2010), ACM Transactions on Graphics, vol. 29, no. 5, pp. 168:1-168:8
Abstract
A central problem in computer graphics is finding optimal sampling conditions for a given surface representation. We propose a new method to solve this problem based on spectral analysis of manifolds which results in faithful reconstructions and high quality isotropic samplings, is efficient, out-of-core, feature sensitive, intuitive to control and simple to implement. We approach the problem in a novel way by utilizing results from spectral analysis, kernel methods, and matrix perturbation theory. Change in a manifold due to a single point is quantified by a local measure that limits the change in the Laplace-Beltrami spectrum of the manifold. Hence, we do not need to explicitly compute the spectrum or any global quantity, which makes our algorithms very efficient. Although our main focus is on sampling surfaces, the analysis and algorithms are general and can be applied for simplifying and resampling point clouds lying near a manifold of arbitrary dimension.Overview
Sampling manifolds defined by points sets is an essential step in the geometry processing pipeline. We propose a new method for sampling point based manifolds. Our method is memory and time efficient, results in high quality samplings and reconstructions, and simple to implement. We assume that we are given a point set and a kernel definition that is used to reconstruct the smooth manifold. The result of our algorithms is an isotropic and adaptive sampling implied by the input point set and the kernel. The distributions of the points have blue noise characteristics. Since we treat manifolds in general, our methods are applicable to Euclidean or high dimensional cases as well. Due to our out-of-core simplification algorithm, we can handle very large datasets. The running time of this algorithm is linear in the number of input points. After simplifying the point cloud data, our resampling algorithm can be used to further optimize the positions of the remaining points.
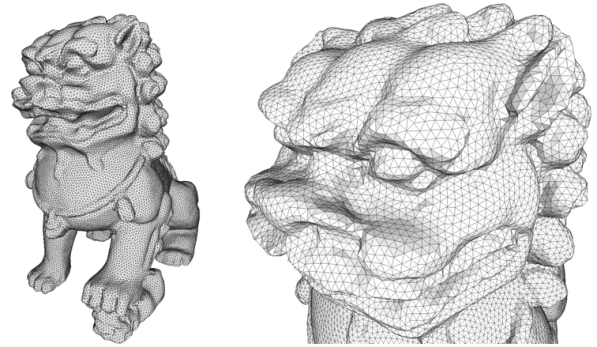
Results
We can get isotropic samplings of a surface using an isotropic kernel definition such as a radially decaying Gaussian.
By adapting the kernel to the features on the surface, adaptive sampling can also be achieved.
If we use our methods to sample a planar domain, we can analyze the distributions and see that they have blue noise properties.
Reconstructions obtained by using the sampled point set is very accurate.
Our samplings can be used to remesh surfaces with high quality triangles.