Analysis and Synthesis of Point Distributions based on Pair Correlation
A. C. Oztireli, M. GrossProceedings of ACM SIGGRAPH Asia (Singapore, November 28 - December 1, 2012), ACM Transactions on Graphics, vol. 31, no. 6, pp. 170:1-170:10
Abstract
Analyzing and synthesizing point distributions are of central importance for a wide range of problems in computer graphics. Existing synthesis algorithms can only generate white or blue-noise distributions with characteristics dictated by the underlying processes used, and analysis tools have not been focused on exploring relations among distributions. We propose a unified analysis and general synthesis algorithms for point distributions. We employ the pair correlation function as the basis of our methods and design synthesis algorithms that can generate distributions with given target characteristics, possibly extracted from an example point set, and introduce a unified characterization of distributions by mapping them to a space implied by pair correlations. The algorithms accept example and output point sets of different sizes and dimensions, are applicable to multi-class distributions and non-Euclidean domains, simple to implement and run in $O(n)$ time. We illustrate applications of our method to real world distributions.Overview
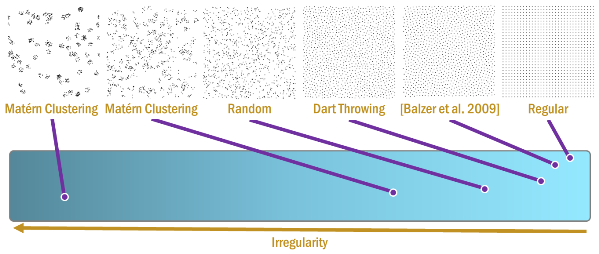
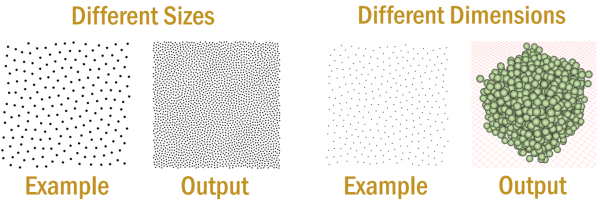
Observing and recreating complex structures and phenomena of the real world is one of the main goals of computer graphics. The structures often exhibit repetitive patterns and symmetries and can be explained well in a distributional sense. Analysis of a specific phenomena is followed by fitting appropriate models and developing specialized algorithms for synthesis. Modeling complex object distributions, turbulence synthesis for fluids, crowd simulations, and many more applications can be seen as instances of this process. Hence, a very important open problem is learning and synthesizing general distributions. In this paper, we introduce methods for analysis and synthesis of general multi-class point distributions based on the statistical measure pair correlation function (PCF). To explore the nature of this measure, we introduce an analysis based on the interpretation of it as a mean in a high dimensional vector space that we call the pair correlation space (PCS). The vector for a given point in the PCS simply measures the distribution of its distance to all other points. We show that in this space, the degrees of freedom to characterize point distributions is low and directly linked to regularity. This analysis allows us to explain distributions and existing synthesis algorithms in a unified way, propose an irregularity measure, and show that the PCF provides a compact representation for the characteristics. Following this analysis, we propose two general synthesis algorithms. The first one is a generalization of dart throwing for arbitrary PCFs and the other is a gradient descent based fitting of the PCFs. The output of the first algorithm is used as the input for the second to facilitate convergence. These algorithms can generate point distributions with desired characteristics extracted from example distributions or synthesized. The example point sets and generated point sets can be of different dimensions and sizes, contain multiple classes, and reside on non-Euclidean domains. The algorithms are simple to implement and run in O(n) time.
Results