Integration with Stochastic Point Processes
A. C. Oztireli(New York, NY, USA, August, 2016), ACM Transactions on Graphics, vol. 35, no. 5, 2016, pp. 160:1--160:16
Abstract
We present a novel comprehensive approach for studying error in integral estimation with point distributions based on point process statistics. We derive exact formulae for bias and variance of integral estimates in terms of the spatial or spectral characteristics of integrands and first- and-second order product density measures of general point patterns. The formulae allow us to study and design sampling schemes adapted to different classes of integrands by analyzing the effect of sampling density, weighting, and correlations among point locations separately. We then focus on non-adaptive correlated stratified sampling patterns and specialize the formulae to derive closed-form and easy-to-analyze expressions of bias and variance for various stratified sampling strategies. Based on these expressions, we perform a theoretical error analysis for integrands involving the discontinuous visibility function. We show that significant reductions in error can be obtained by considering alternative sampling strategies instead of the commonly used random jittering or low discrepancy patterns. Our theoretical results agree with and extend various previous results, provide a unified analytic treatment of point patterns, and lead to novel insights. We validate the results with extensive experiments on benchmark integrands as well as real scenes with soft shadows.
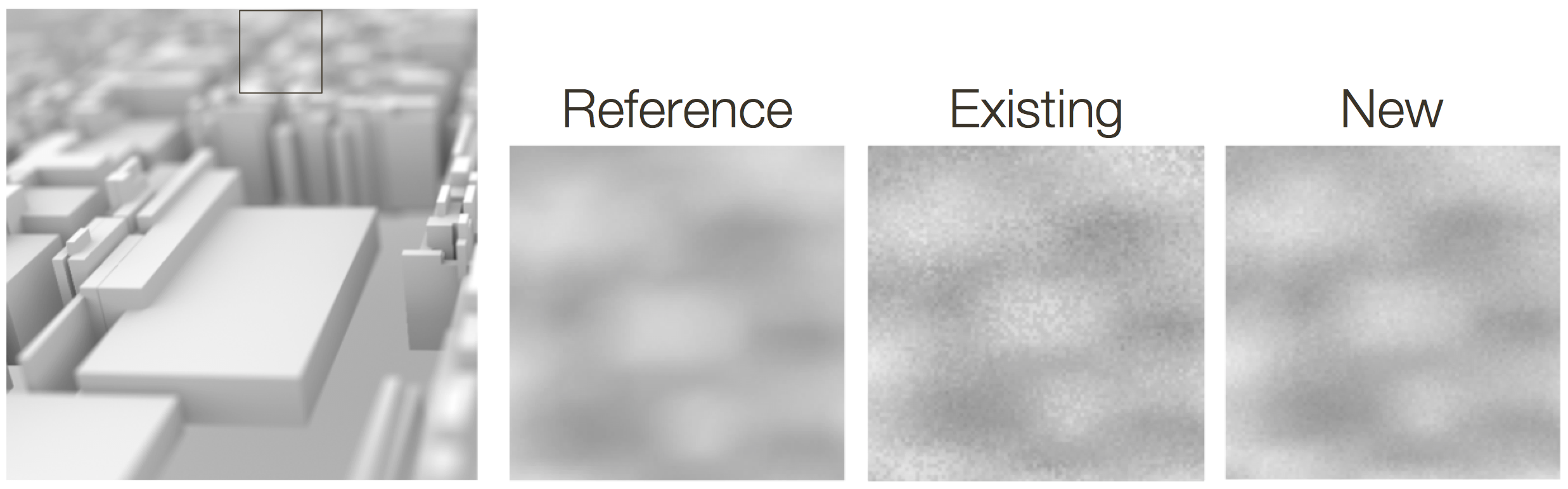
Overview
We present a novel comprehensive approach for studying error in integral estimation with point distributions based on point process statistics. We derive exact formulae for bias and variance of integral estimates in terms of the spatial or spectral characteristics of integrands and first- and-second order product density measures of general point patterns. The formulae allow us to study and design sampling schemes adapted to different classes of integrands by analyzing the effect of sampling density, weighting, and correlations among point locations separately. We then focus on non-adaptive correlated stratified sampling patterns and specialize the formulae to derive closed-form and easy-to-analyze expressions of bias and variance for various stratified sampling strategies. Based on these expressions, we perform a theoretical error analysis for integrands involving the discontinuous visibility function. We show that significant reductions in error can be obtained by considering alternative sampling strategies instead of the commonly used random jittering or low discrepancy patterns. Our theoretical results agree with and extend various previous results, provide a unified analytic treatment of point patterns, and lead to novel insights. We validate the results with extensive experiments on benchmark integrands as well as real scenes with soft shadows.

