Lagrangian Vortex Sheets for Animating Fluids
T. Pfaff, N. Thuerey, M. GrossProceedings of ACM SIGGRAPH (Los Angeles, USA, August 5-9, 2012), ACM Transactions on Graphics, vol. 31, no. 4, pp. 112:1-112:8
Abstract
Buoyant turbulent smoke plumes with a sharp smoke-air interface, such as volcanic plumes, are notoriously hard to simulate. The surface clearly shows small-scale turbulent structures which are costly to resolve. In addition, the turbulence onset is directly visible at the interface, and is not captured by commonly used turbulence models. We present a novel approach that employs a triangle mesh as a high-resolution surface representation combined with a coarse Eulerian solver. On the mesh, we solve the interfacial vortex sheet equations, which allows us to accurately simulate buoyancy induced turbulence. For complex boundary conditions we propose an orthogonal turbulence model that handles vortices caused by obstacle interaction. In addition, we demonstrate a re-sampling scheme to remove surfaces that are hidden inside the bulk volume. In this way we are able to achieve highly detailed simulations of turbulent plumes efficiently.Overview
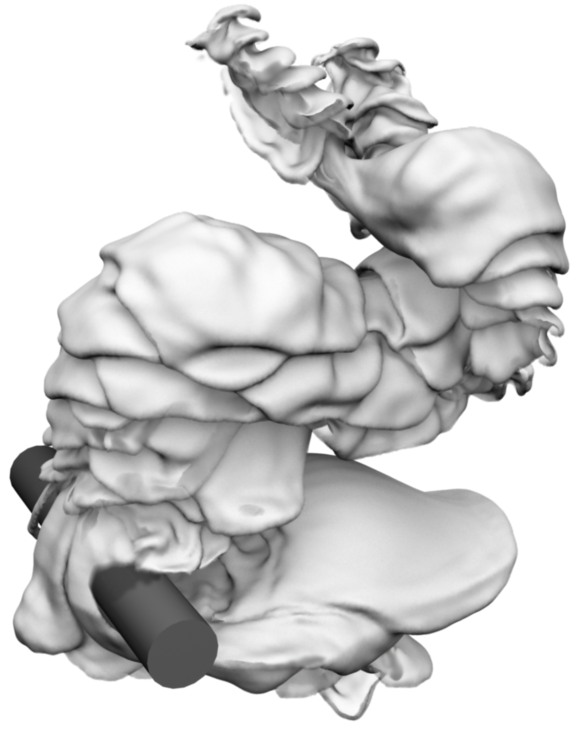
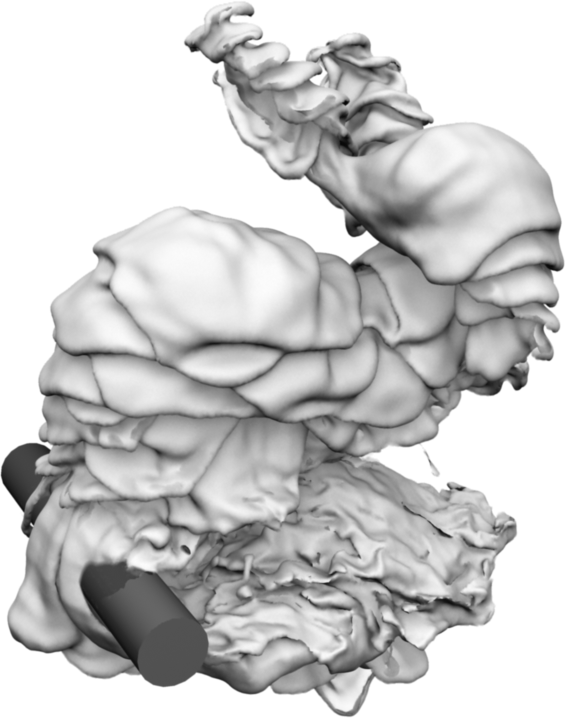
Turbulent dense smoke clouds, such as volcanic plumes, are very hard to simulate. First, they require very high simulation resolutions to represent the high level of visible detail on a large body of smoke. Worse yet, turbulence methods, which are typically used in such scenarios to provide cheap subgrid detail, will not work for dense buoyant plumes (Fig. 2). The reason for this is that the characteristic shape of these clouds are defined by slow turbulence transition processes acting on the smoke surface, and these processes are not easily captured using statical turbulence methods.
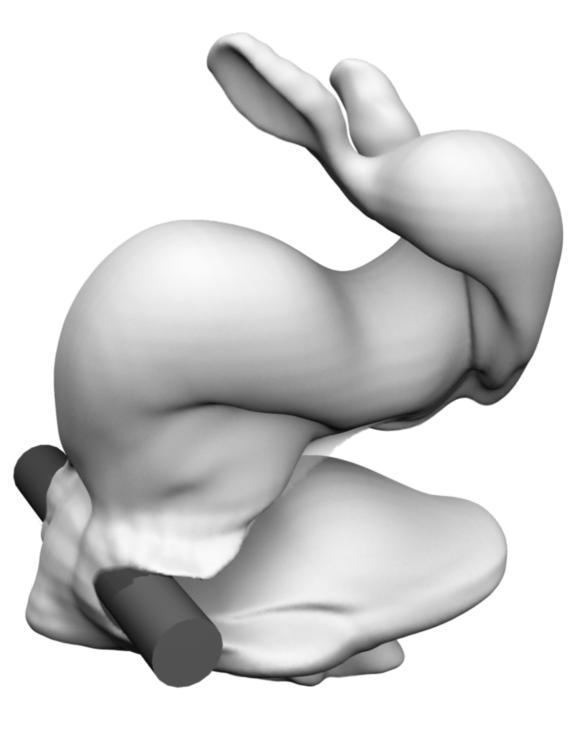
In our approach, we use a Lagrangian traingle mesh to track the interface surface between the dense smoke cloud and air. This enables large, highly detailed smoke plumes without a costly high-resolution volumetric representation. We show that we can calculate the fluid motion including detailed turbulence transition effects directly on this surface mesh using vortex sheets dynamics. To improve performance, a low-resolution grid-based base solver is used for to calculate far-field effects and the interaction with flow boundary conditions. We combine our vortex sheet approach with a turbulence model to incorporate turbulence generation from obstacles (Fig. 1).
Source code
Our method is implemented using mantaflow, an open-source fluid solver framework. Currently, only our base solver is included, but the complete source code of our method will be available soon with the next public version of mantaflow. URL: http://mantaflow.ethz.ch