Two-Scale Particle Simulation
B. Solenthaler, M. GrossProceedings of ACM SIGGRAPH (Vancouver, Canada, August 7-11, 2011), ACM Transactions on Graphics, vol. 30, no. 4, pp. 81:1-81:8
Abstract
We propose a two-scale method for particle-based fluids that allocates computing resources to regions of the fluid where complex flow behavior emerges. Our method uses a low- and a high-resolution simulation that run at the same time. While in the coarse simulation the whole fluid is represented by large particles, the fine level simulates only a subset of the fluid with small particles. The subset can be arbitrarily defined and also dynamically change over time to capture complex flows and small-scale surface details. The low- and high-resolution simulations are coupled by including feedback forces and defining appropriate boundary conditions. Our method offers the benefit that particles are of the same size within each simulation level. This avoids particle splitting and merging processes, and allows the simulation of very large resolution differences without any stability problems. The model is easy to implement, and we show how it can be integrated into a standard SPH simulation as well as into the incompressible PCISPH solver. Compared to the single-resolution simulation, our method produces similar surface details while improving the efficiency linearly to the achieved reduction rate of the particle number.Overview
The physical and visual quality of particle-based solvers like SPH are defined by the number of particles that are used to discretize the fluid. Generally, the more particles that are used, the smaller the damping artifacts and the more small-scale details like splashes, spray, and surface waves can be reproduced. However, doubling the resolution of a simulation increases the particle number by a factor of 8. This increases the computational cost notably since it depends linearly on the number of particles.
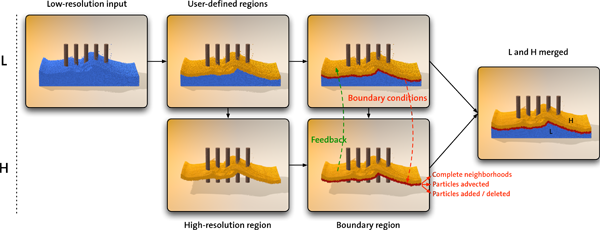
To cope with the increasing demand for more detailed flow structures, we propose a new level-of-detail technique that follows the idea to allocate computing resources to regions where complex flow behavior emerges. Instead of recursively subdividing particles which results in particles of different sizes that interact with each other, we rather use a hierarchy of different resolution levels. While the number of resolution levels is not fundamentally limited with our method, we focus on two scales only.
We use two distinct but coupled simulations; one simulation that computes the whole fluid with a coarse resolution L (blue), and a high-resolution level H that simulates a subset of the fluid with small particles (yellow). Boundary conditions (red) are defined, and feedback forces from H onto L are included. The particles of both simulations can then be merged for the final rendering. An overview of our method is shown in Figure 1.
Results
Our method can stably handle dynamically changing and complex high-resolution regions. We present several examples in the paper using different sampling criteria. Figure 2 shows an example where the area around cylindrical obstacles is computed with quadrupled resolution (factor 64 smaller particles) to get small-scaled splashes and individual droplets at impact locations. In this particular example, our method reduces the total particle number and hence the overall computational cost by a factor of 6.7 compared to the single-scale reference simulation.
The result is visually compared to the single-scale reference simulation in Figure 3, showing that our method produces very similar flow details.