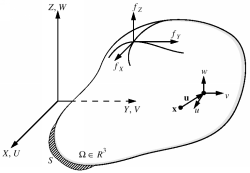
Introduction

The analysis of soft tissue requires the idealization of tissue into a form that can be solved, the formulation of the mathematical and physical model, and the interpretation of the results. In our approach to soft tissue simulation we think of tissue as being elastic and therefore base on the theory of static elastomechanics. As for all continuous-system mathematical models, the governing differential equations must hold throughout the domain of the system.

Underlying Physics

In order to derive the governing differential equations, we follow the variational approach, which essentially calculates the total potential P of the system - the functional of the problem - and invokes the stationarity of P, which is equivalent to finding the configuration of minimal potential energy. In elastomechanics the potential P can be regarded as the elastic energy of the body minus the work done by externally applied forces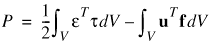

where epsilon and tau denote strain and stress respectively.

where the overbars on u and epsilon denote virtual displacements and corresponding virtual strains respectively. This equilibrium equation can be obtained by invoking the stionarity of the potential P.

Finite Element Discretization

The discretization in the Finite Element Method consists of two main aspects: firstly, the domain of interest is subdivided into a finite and disjoint set of primitives, so-called finite elements, and secondly, we expand the solution u within an element m as a weighted sum of n basis or shape functions . This process is known as Galerkin projection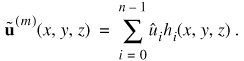

Using the Galerkin projection yields a matrix formulation of the problem for one element. Integrating over each element and summing up the contribution of each element into one global system of linear equations - a process referred to as the finite element assembly - yields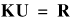

where K denotes the global stiffness matrix, U represents the global weight vector we are solving for and R stands for the global load vector.

Current Approaches

Currently, two approaches are under investigation: On the one hand, we devised a new set of rational prismatic shape functions featuring a globally C1-continuous surface in combination with a C0 interior. Not only is it numerically accurate, but this construction enables us to compute smooth and visually appealing facial shapes. The development of a first prototype using this approach yielded very promising results examples of which can be found in the Image Gallery and Videos sections.

On the other hand, a tetrahedral approach offering full global C1-continuity is in the process of development. This approach, as general in topology and geometry as possible, will also combine nonlinear elasticity with incompressibility in order to model more accurately the complex behavior of human facial soft tissue. In this approach, Bernstein-Bézier based tetrahedral shape functions allow for analytical integration instead of using Gaussian quadrature, but require a highly complex assembly procedure which takes into account the linear dependencies implied by the continuity constraints between adjacent elements.