Computer Graphics Laboratory

CGL » Research » Visualization

Visualization

Introduction

Vector field visualization is a major discipline of scientific visualization that helps to push the frontiers of research in fluid mechanics, medicine, biology, astrophysics and many more. Our goal is to develop novel algorithms that help to extract features in flows, such as vortices or separating structures. We improve the rendering quality to increase the reliability of the obtained visualizations, and we put the users first to let them emphasize and discover certain structures of interest. We investigate the properties of traditional flows such as gases and fluids, as well as higher-dimensional flows that describe the motion of finite-sized objects carried by fluids, also known as inertial particles.

Topics

Feature Extraction in Unsteady Flows

Our research is dedicated to novel extraction and rendering techniques for the visualization of features in unsteady flows. For this, we apply techniques from light transport in heterogeneous participating media to the unbiased rendering of features in Lagrangian scalar fields. An example in atmospheric flows are the ridges of the finite-time Lyapunov exponent (FTLE), which constrain the advection of trace gases, guide temperature diffusion, and cloud formation.


Inertial Particle Dynamics

Recent research in flow visualization focused on the analysis of massless particles. However, in many application scenarios, the mass of particles and their resulting inertia are essential, for instance when sand particles interact with aircraft. The governing ordinary differential equation of even simple inertial flow models is up to seven dimensional, which makes feature extraction a challenging task. We extract and visualize integral geometry, study the vortical motion and separation behavior of inertial particles, and extend traditional vector field topology to the inertial case.


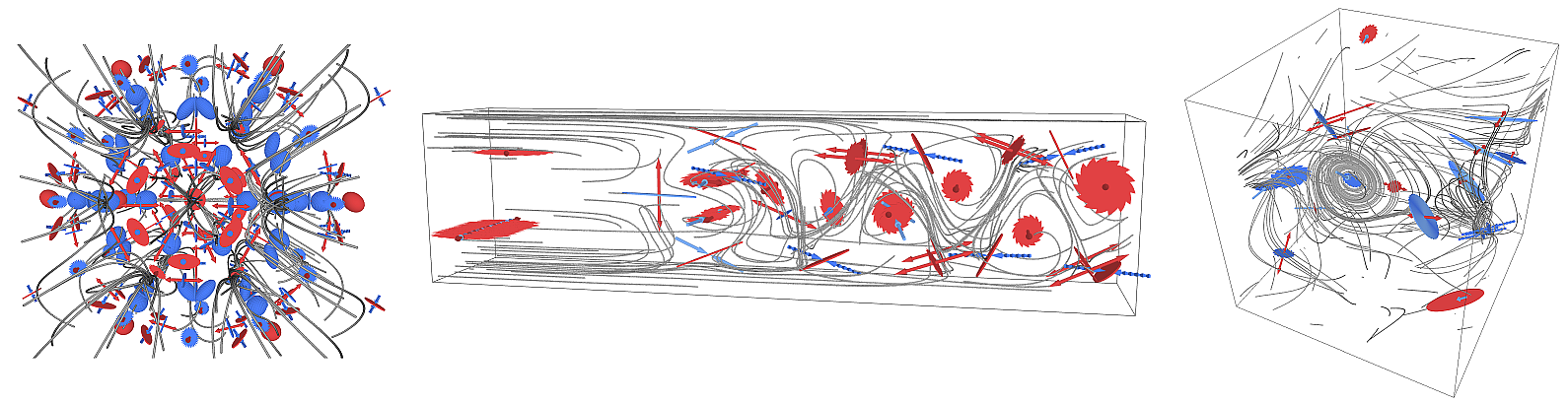
Optimal Reference Frames for Vortex Extraction

Vortex extraction is among the most challenging tasks of vector field analysis. We investigate elegant optimization-based approaches that extract vortices in an optimal near-steady reference frame. Vortex measures thereby become invariant under initial rotations and translations of the observer, i.e., they become objective.


Visibility Optimization

When it comes to 3D flow visualization, we often encounter occlusion problems when displaying dense sets of points, lines or multiple surfaces. A vital aspect is the careful selection of the primitives that best communicate the relevant features in a data set. We investigate optimization-based approaches that adjust the opacity of points, lines and surfaces to strive for a balance between the presentation of relevant information and occlusion avoidance.


Publications





© 2024 ETH Zurich, Computer Graphics Laboratory